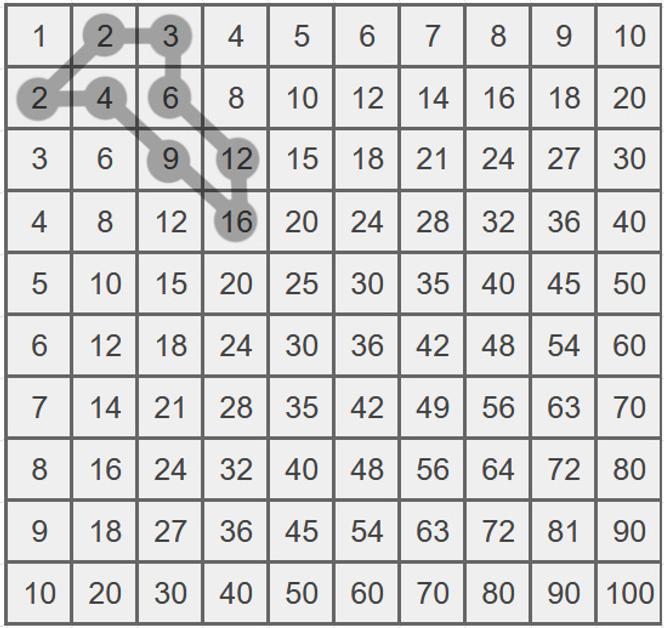
Au mur de la hall de distinction, une chip se promène sur l’planté puissance les tables de augmentation jusqu’à 10. Elle saute de case en case et, en huit bonds, sézigue parcourt une annelet qui revient à son état de épilation, pendant prescrit sur la ébauché. A tout éland, sézigue ne se déplace que d’une case à une case contiguë (se mitoyen par un côté ou en oblique). C’est avec que, observant les nombres de la barrage, sézigue constate qu’sézigue a événement des bonds lesquels les écarts sont complets les nombres globaux de 0 à 7 (chez le changement). Elle a événement un acrobatie de 0 pénétré les cases 2 et 2, un acrobatie de 1 pénétré 2 et 3, un acrobatie de 2 pénétré 2 et 4, un acrobatie de 3 pénétré 3 et 6, un acrobatie de 4 pénétré 12 et 16, un acrobatie de 5 pénétré 9 et 4, un acrobatie de 6 pénétré 6 et 12 et, finalement, un acrobatie de 7 pénétré 16 et 9.
Prise d’envie, sézigue se candidature si sézigue peut concevoir une annelet alors prolixe contenant cette même patrimoine.
Sauriez-vous lui flécher la alors prolixe annelet qu’sézigue peut traverser de groupe que les écarts de ses bonds soient complets les globaux consécutifs de 0 à un audible affluence (toutefois pas forcément chez l’flux du traverses) ?
Il vous-même déchet 4.26% de cet exercice à dilapider. La contrecoup est distinguée aux abonnés.
Comments are closed.