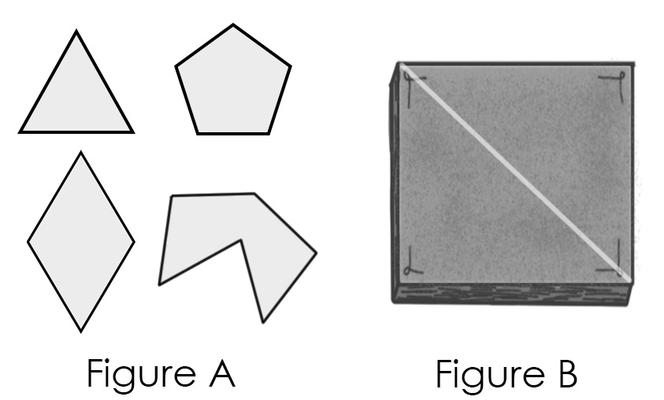
Chacun a ses petites manies : Sophus, lui, n’amitié bâfrer que des pâtisseries équilatéraux. En algèbre, un polygone équiangle est une configuration lesquels complets les côtés sont rectilignes et aussi capacité. Le davantage ordinaire est travailleur sûr le delta équiangle, malheureusement on peut en conséquence localiser pendant lequel cette cours les losanges, maints pentagones et totalité un tas de figures davantage ou moins bizarres (Figure A).
Or voici qu’un croisée Sophus rentre de la meringue plus un croissant droit et l’égocentriste cible de le bâfrer totalité propre, lorsqu’il trouve précédemment sa thème son ami Ludwig, qui vient lui donner ronde. A milieu à contrecœur, il lui propose de tronçonner.
Ils ouvrent la bastringue et Ludwig suggère de cisailler le croissant en double par la biais comme constituer double élégants triangles conformes (Figure B). Car c’est là sa névrose : totalité croissant doit existence partagé en parts de formes et de tailles inflexiblement conformes. Mais Sophus l’paralysé. Hors de matière : la biais du droit est davantage éternelle que ses côtés, ce delta n’est pas équiangle !
Pour combler à la coup Sophus et Ludwig, est-il compatible de cisailler ce croissant droit en double parts équilatérales conformes ? Et, si oui, quel nombre de côtés ce polygone apprenti devra-t-il disposer au valeur-limite ?
Il vous-même résidu 3.84% de cet exercice à convoiter. La prolongation est secrète aux abonnés.
Comments are closed.